Above: A three-dimensional section through the Great
Prismosaurus—a uniform star-polychoron whose cells are
720 highly intersecting congruent pentagonal prisms. This
star-polychoron is highly nonconvex!! The section is orthogonal
to an icosahedral symmetry axis by a realm passing through the figure 15% of the way
out from the center toward a vertex. This polychoron was
discovered independently by me in 1997 and (somewhat earlier) by
Jonathan Bowers of Tyler, Texas, and this website is its
“public debut.” It is one of 8190 currently known
uniform polychora, many of which are simpler but most of which
are much more complicated. Jonathan has discovered more than 8000
of these during the past decade, working—in the tradition of
Ludwig Schläfli, Thorold Gosset, and Alicia Boole
Stott—independently and in virtual isolation.
The most recent changes to the roster of uniform polychora
begin with two odd figures having the symmetry of a
square-octagonal duoprism that Jonathan discovered in January
2002. These had been sitting under our noses for years; we should
have found them long ago. They brought the polychora count up to
8188. Then in April 2002, after corresponding with Japanese
geometer Hironori Sakamoto, Jonathan removed four figures that
turned out to be degenerate, bringing the count down to 8184. But
later that month, Hironori discovered four new uniform facetings
in an existing regiment, and Jonathan found two more related to
those. This brought the count up to 8190, as high as it has ever
been. Details are available at Jonathan’s website (link in
following digressive paragraph).
[Regarding Jonathan Bowers, from December 12, 1999 through
January 2, 2000 I added his alternative names for the convex
uniform polychora to the tables. See the Nomenclature section for details. Jonathan
now has a website where he displays
some of his wonderful POVray-rendered
three-dimensional cross-sections of various uniform polychora.
His classification of the known uniform polychora into 29 groups
also appears there.]
The Great Prismosaurus has 120 vertices, 1200
edges, 1800 square faces, and 720 pentagonal faces to connect its
720 pentagonal-prism cells together. Sixty cells come together at
each vertex. The squares are also the faces of a uniform
compound of 75 tesseracts, while the pentagons are also
the faces of the regular star-polychoron
{5,5/2,3}, the
great grand hecatonicosachoron. Both of these figures of
course have the same sets of vertices and edges as the Great
Prismosaurus.
All the edges are surrounded alike by nine prisms, which makes
the Great Prismosaurus not only uniform but quasi-regular;
and since it has only one kind of cell, it is also
isochoric. If you look closely at the figure, you will see
that nine intersecting face planes meet at every
corner—the sections of the nine prisms that surround each
edge in the polychoron. The prisms are quite large relative to
the size of the polychoron itself, and they pass quite close to
the center. The dihedral angle between two prisms at a common
pentagonal face is 36°, and if you travel from prism to prism
across the parallel pentagonal bases, you’ll pass through
five before returning to your starting point, after going twice
around the polychoron. If you travel from prism to prism around a
common edge, you’ll circle the edge four times in passing
through the nine prisms that share that edge. In the section
shown, all the vertices are sections of various edges, and all
the faces are sections of various cells: the sectioning realm
bypasses the polychoron’s own vertices.
I estimate that this section of the Great Prismosaurus
(Greekish name: pentagonal-prismatic heptacosiicosachoron)
has on the order of 400,000 facelets, which a polyhedron
model-maker would have to cut out and paste together to make a
paper model. Many are very small—at or below the limits of
the picture resolution for a picture this size. Each facelet
is the section of a corresponding cellet in the
exterior of the Great Prismosaurus. A hypothetical
four-dimensional model-maker, or HM[4], would have to precisely
cut out (from three-dimensional cardboard) and glue together more
than a million cellets to build a model of this polychoron. And
this one is nowhere near as complicated as some of the known
uniform star-polychora become.
The Great Prismosaurus has a simpler conjugate: a uniform
polychoron whose cells are 720 pentagrammatic prisms. It is the
simpler of the two polychora because it has far fewer
self-intersections, so we call it the Small Prismosaurus;
its Greekish name would be pentagrammatic-prismatic
heptacosiicosachoron. It has the same vertices, edges, and
square faces as the Great Prismosaurus, but the pentagons are
discarded and replaced by the pentagrams of the regular
star-polychoron {5/2,5,3}, the stellated
hecatonicosachoron (which has the same vertices and edges as
the great grand hecatonicosachoron and both Prismosauri).
The most recent additions to the roster of uniform polychora
are the Prismosaurus Hybrids: a sequence of six prismlike
uniform polychora that “fit in between” the Small and
Great Prismosaurus. In the first Hybrid, 120 pentagrammatic
prisms (twelve girdles of ten, or, more accurately, 24 girdles of
five compounded pairwise) of the Small Prismosaurus are exchanged
for 120 pentagonal prisms of the Great Prismosaurus. In the
second, another set of 120 prisms is exchanged. There are two
ways to uniformly exchange three sets of 120, there is one way to
exchange four sets of 120, and one final way to exchange five
sets. If you exchange all six sets of 120 prisms of the Small
Prismosaurus, you get the Great Prismosaurus, of course. The
Hybrids are less symmetric than the Prismosauri themselves, but
they are nevertheless still uniform. Each Hybrid is
chiral—it comes in left-handed and right-handed
forms—as is its vertex figure. The Hybrids are six of ten
known polychora I call swirlprisms (and Norman Johnson
calls chiroprisms) that I discovered during August and
September 1999. They are the only known chiral uniform polychora
that also have chiral vertex figures. We expect to turn up more
of these as we get the hang of working with chiral symmetries in
four-space. To see five views of each Hybrid Prismosaurus vertex
figure, constructed by Jonathan Bowers, click here: Hybrid swirlprism vertex figures. To see
pictures of the chiral vertex figures of the first four
swirlprisms, click here: Swirlprism vertex
figures. To see a set of three-dimensional sections
of the simplest swirlprism (the sisp), click here: Small swirlprism sections, vertex first, part 1
(from vertex to center); and here: Small
swirlprism sections, vertex first, part 2 (continuing from center
to opposite vertex). The small swirlprism has 120 pentagonal
antiprisms for its cells (one of which pops into existence in the
.100 section in part 1, another symmetrically pops out after the
.900 section in part 2). These sections clearly show why I called
these polychora swirlprisms!
The small swirlprism was sectioned by Jonathan Bowers using
his POV-ray uniform polychoron sectioning system, and I added it
to this website May 12, 2001. The Great Prismosaurus picture was
produced by Bruce L. Chilton of
Tonawanda, New York using his four-dimensional sectioning program
and the Imagine three-dimensional graphic display system. He is
the one who named it the Prismosaurus. The original colors were
inverted for this composition by Joel McVey of San Diego,
California. I added this picture to this website August 18, 1998.
Bruce recently produced motion pictures of all twelve regular
pentagonal polychora—two convex and ten
star-polychora—as well as the Great Prismosaurus, as MPG
files. The polychora appear as changing polyhedral sections, as
we would see them if they were passing through our real
three-space at a uniform rate.
In succeeding months, I will begin to post information on the
other nonconvex uniform polychora, as well as more basic and
introductory matter related to the geometry of four-dimensional
space. Meanwhile, information on all the convex uniform polychora
may be found by clicking on the hyperlinks at the end of this
page. Ultimately, I’d like to create an illustrated Web page
for each different uniform polychoron, convex and nonconvex, but
this would take about 15 years’ work and require about a
gigabyte of disk space!
Indexing sets of things seems to be in my blood: My present
“day job” is professionally indexing books of all kinds
as a freelancer. My Dinosaur
Genera List website is essentially an index to all the
dinosaur names, and this Uniform Polychora website you are
now visiting is, likewise, an index to all the convex uniform
polychora. Just to keep my verbal skills intact, I do each
day’s New York Times crossword puzzle. During the
early 1990s I served two years as president of the San Diego
Stamp Club, but I’m not currently an active stamp
collector. (Over the course of some 40 years, I had assembled
nearly complete collections of Poland, France, and United States
postage and revenue stamps, and filling my want lists just became
too expensive! I do keep up my membership in the American
Philatelic Society, however, just in case I ever return to stamp
collecting.)
[Additions, corrections, and suggestions are always welcome.
I continue to make minor modifications and adjustments, weeding
out occasional typographical errors and so forth. When I’m
satisfied, I’ll remove this bracketed note. On
November 18, 1998, I added as a test the first of my
vertex-figure illustrations, for polychoron #15 in Section 2. By
January 5, 1999, all sections of the table were fully
illustrated. The prism section, Section 6, pictures 36 vertex
figures and takes more than twice as long to download as Sections
1–5; Section 7, all of whose polychora are duplicates of
others in the table, needs no illustrations. The numerals on the
edges in the pictures denote the number of sides of the
corresponding regular-polygonal faces at a vertex of the
polychoron; the length of an edge labeled p is thus
2cos(pi/p). Mathematica 2.1 uses 8-bit
color, which is why the pictures suffer from dither, but I think
this is not a terrible problem because the vertex figures are
rather simple polyhedra.
In 1996, an old high-school friend sent me a copy of Roman
Maeder’s terrific article “Uniform Polyhedra” from
Mathematica Journal 3(4), 1993. This inspired me to dredge
up some old notes I’d made in the 1960s on the convex
uniform polychora. Long ago, Bruce
Chilton introduced me to the Coxeter-Dynkin system for
performing Wythoff’s construction, which makes discovering
Wythoffian uniform polytopes and extracting some of their
properties quite simple, and I used the system to enumerate these
polychora. I’ve also discovered or rediscovered quite a few
Wythoffian uniform star-polychora, but my comments on them must
wait until my notes become more coherent. Many of those
star-polychora—the four-dimensional versions of the
nonconvex uniform polyhedra enumerated by Coxeter,
Longuet-Higgins, and Miller in 1954—are incredibly
complicated: note the picture at the beginning of this Web page!
To see a plane projection of a regular star-polychoron—a
computer drawing I made for Coxeter’s book Regular
Complex Polytopes—go to this web site: great
stellated hecatonicosachoron.
Now let me digress. Just for the record, and for comparison
with the polychoric names, here are the names, symmetry groups,
and most frequently used Schläfli symbols and
Wythoff symbols of the 18 convex nonprismatic uniform
polyhedra. Optional names or parts of names are [bracketed]. The
pictures of the polyhedra, added May 30, 2001 and revised June 2,
2001, were drawn by Jonathan Bowers using his POV-ray system, and
include his “shortcut” names for them. Here HTML forces
compromises: For uniform polyhedra whose Schläfli symbols
are usually written vertically I adopt Norman Johnson’s
convention of using an r (for “rectified”) in front of
the symbol. The Coxeter-Dynkin graphs for all the convex uniform
polyhedra appear at the end of Section 6 on prismatic polychora
as the first three nodes of the graphs of the corresponding
uniform-polyhedral prisms. And the (polygonal) vertex figures of
all the convex uniform polyhedra appear there as the bases
of the pyramidal vertex figures of their polyhedral prisms!
The regular polyhedra have been known since before the time of
the classical Greeks, and were studied by the Pythagoreans and by
Plato, so they’re often called the Platonic
polyhedra. (For a quick look at my models of all nine regular
polyhedra, convex and nonconvex, click on Regular
Polyhedra photo.) The uniform polyhedra with more than one
kind of face were, according to many accounts, first enumerated
by Archimedes, so they are likewise called the Archimedean
polyhedra. Here, and everywhere in the tables, all the
polytopes are assumed to be regular and/or uniform unless
specifically denoted otherwise. Vertex figures, however, are
not regular or uniform unless specifically denoted as
such; their size assumes an Archimedean polytope of unit edge
length. Outside the context of these tables, it may be necessary
to add the qualifiers “regular” or “uniform”
to the names to distinguish them from nonuniform polychora with
identical cell counts.
A. Regular or Platonic polyhedra (uniform polyhedra with
one kind of face):
1. Tetrahedron
[4 vertices, 6 edges, 4 triangular faces]
Vertex figure: Equilateral triangle, edge 1
Schläfli symbols: {3,3} or sr{2,2}
Wythoff symbols: 3 | 2 3 or | 2 2 2
Symmetry group: Tetrahedral [3,3], of order 24
In nonprismatic convex uniform polychora, can appear with
triangular pyramidal symmetry (in snub icositetrachoron), and
bilateral symmetry of order 2 and direct digonal-dihedral
symmetry of order 4 (both kinds in grand antiprism), as well as
with tetrahedral symmetry
2. Cube [hexahedron]
[8 vertices, 12 edges, 6 square faces]
Vertex figure: Equilateral triangle, edge sqrt(2)
Schläfli symbols: {4,3}, t{2,4}, or tr{2,2}
Wythoff symbols: 3 | 2 4, 2 4 | 2, or 2 2 2 |
Symmetry group: Octahedral [3,4], of order 48
In nonprismatic convex uniform polychora, can appear with
square dihedral symmetry [2,4] of order 16 as well as with
octahedral symmetry
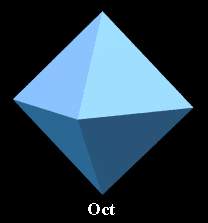3. Octahedron
[6 vertices, 12 edges, 8 triangular faces]
Vertex figure: Square, edge 1
Schläfli symbols: {3,4}, r{3,3}, sr{2,3}, or s{3}h{ }
Wythoff symbols: 4 | 2 3, 2 | 3 3, or | 2 2 3
Symmetry group: Octahedral [3,4], of order 48
In nonprismatic convex uniform polychora, can appear with
tetrahedral symmetry as well as with octahedral symmetry
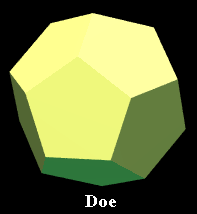4. Dodecahedron
[20 vertices, 30 edges, 12 pentagonal faces]
Vertex figure: Equilateral triangle, edge tau
Schläfli symbol: {5,3}
Wythoff symbol: 3 | 2 5
Symmetry group: Icosahedral [3,5], of order 120
5. Icosahedron
[12 vertices, 30 edges, 20 triangular faces]
Vertex figure: Regular pentagon, edge 1
Schläfli symbol: {3,5}
Wythoff symbol: 5 | 2 3
Symmetry group: Icosahedral [3,5], of order 120
In nonprismatic convex uniform polychora, can appear with
pyritohedral symmetry [3+,4] of order 24 (in snub
icositetrachoron) as well as with icosahedral symmetry
B. Quasi-regular Archimedean polyhedra (uniform polyhedra
with two different kinds of faces but equivalent edges):
6. Cuboctahedron
[12 vertices, 24 edges, 8 triangular and 6 square faces]
Vertex figure: Rectangle, edges 1 and sqrt(2)
Schläfli symbols: r{4,3}, r{3,4}, or rr{3,3}
Wythoff symbol: 2 | 3 4 or 3 3 | 2
Symmetry group: Octahedral [3,4], of order 48
In nonprismatic convex uniform polychora, can appear with
tetrahedral symmetry as well as with octahedral symmetry
7. Icosidodecahedron
[30 vertices, 60 edges, 20 triangular and 12 pentagonal
faces]
Vertex figure: Rectangle, edges 1 and tau
Schläfli symbols: r{5,3} or r{3,5}
Wythoff symbol: 2 | 3 5
Symmetry group: Icosahedral [3,5], of order 120
C. Semi-regular Archimedean polyhedra (uniform polyhedra
with at least two different kinds of faces and inequivalent
edges):
8. Truncated tetrahedron
[12 vertices, 18 edges, 4 triangular and 4 hexagonal faces]
Vertex figure: Isosceles triangle, base 1, lateral sides
sqrt(3)
Schläfli symbol: t{3,3}
Wythoff symbol: 2 3 | 3
Symmetry group: Tetrahedral [3,3], of order 24
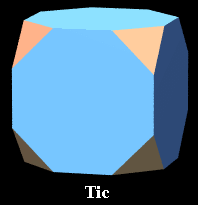9. Truncated cube
[24 vertices, 36 edges, 8 triangular and 6 octagonal faces]
Vertex figure: Isosceles triangle, base 1, lateral sides
sqrt[2+sqrt(2)]
Schläfli symbol: t{4,3}
Wythoff symbol: 2 3 | 4
Symmetry group: Octahedral [3,4], of order 48
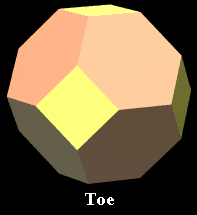10. Truncated octahedron
[24 vertices, 36 edges, 6 square and 8 hexagonal faces]
Vertex figure: Isosceles triangle, base sqrt(2),
lateral sides sqrt(3)
Schläfli symbols: t{3,4} or tr{3,3}
Wythoff symbols: 2 4 | 3 or 2 3 3 |
Symmetry group: Octahedral [3,4], of order 48
In nonprismatic convex uniform polychora, can appear with
tetrahedral symmetry as well as with octahedral symmetry
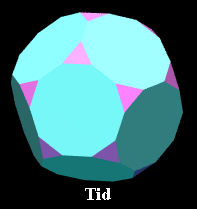11. Truncated dodecahedron
[60 vertices, 90 edges, 20 triangular and 12 decagonal faces]
Vertex figure: Isosceles triangle, base 1, lateral sides
sqrt(2+tau)
Schläfli symbol: t{5,3}
Wythoff symbol: 2 3 | 5
Symmetry group: Icosahedral [3,5], of order 120
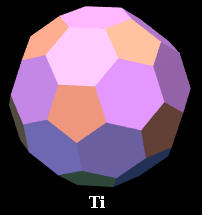12. Truncated icosahedron
[60 vertices, 90 edges, 12 pentagonal and 20 hexagonal faces]
Vertex figure: Isosceles triangle, base tau, lateral
sides sqrt(3)
Schläfli symbol: t{3,5}
Wythoff symbol: 2 5 | 3
Symmetry group: Icosahedral [3,5], of order 120
13. [Small] rhombicuboctahedron
[24 vertices, 48 edges, 8 triangular and 18 square faces]
Vertex figure: Equilateral trapezoid, base 1, the other three
sides sqrt(2)
Schläfli symbols: rr{4,3} or rr{3,4}
Wythoff symbol: 3 4 | 2
Symmetry group: Octahedral [3,4], of order 48
14. [Small] rhombicosidodecahedron
[60 vertices, 120 edges, 20 triangular, 30 square, and 12
pentagonal faces]
Vertex figure: Isosceles trapezoid, one base 1, one base
tau, lateral sides sqrt(2)
Schläfli symbols: rr{5,3} or rr{3,5}
Wythoff symbol: 3 5 | 2
Symmetry group: Icosahedral [3,5], of order 120
15. Truncated cuboctahedron [great rhombicuboctahedron]
[48 vertices, 72 edges, 12 square, 8 hexagonal, and 6
octagonal faces]
Vertex figure: Scalene triangle, sides sqrt2,
sqrt(3), sqrt[2+sqrt(2)]
Schläfli symbols: tr{4,3} or tr{3,4}
Wythoff symbol: 2 3 4 |
Symmetry group: Octahedral [3,4], of order 48
16. Truncated icosidodecahedron [great
rhombicosidodecahedron]
[120 vertices, 180 edges, 30 square, 20 hexagonal, and 12
decagonal faces]
Vertex figure: Scalene triangle, sides sqrt(2),
sqrt(3), sqrt(2+tau)
Schläfli symbols: tr{5,3} or tr{3,5}
Wythoff symbol: 2 3 5 |
Symmetry group: Icosahedral [3,5], of order 120
17. Snub cuboctahedron
[24 vertices, 60 edges, 32 triangular and 6 square faces;
chiral]
Vertex figure: Bilaterally symmetric pentagon, four sides 1,
the fifth side sqrt(2)
Schläfli symbols: sr{4,3} or sr{3,4}
Wythoff symbol: | 2 3 4
Symmetry group: Direct octahedral [3,4]+, of order 24
Does not occur as a cell of any nonprismatic convex uniform
polychoron
18. Snub icosidodecahedron
[60 vertices, 150 edges, 80 triangular and 12 pentagonal
faces; chiral]
Vertex figure: Bilaterally symmetric pentagon, four sides 1,
the fifth side tau
Schläfli symbols: sr{5,3} or sr{3,5}
Wythoff symbol: | 2 3 5
Symmetry group: Direct icosahedral [3,5]+, of order 60
Does not occur as a cell of any nonprismatic convex uniform
polychoron
Also Archimedean are the p-gonal prisms
t{2,p} or {p}x{ }, or 2 p | 2, and
antiprisms sr{2,p} or s{p}h{ }, or | 2 2
p. There are an infinite number of these, one of each for
each integer p>2. For p=3, the antiprism is a
regular octahedron, and for p=4, the prism is a cube. In
this discussion, the letters n, p, and q are
always nonnegative integers. Below are tabulated the six
Archimedean prisms and antiprisms that occur as cells of the
nonprismatic convex Archimeadean polychora.
Triangular prism
[6 vertices, 9 edges, 2 triangular and 3 square faces]
Vertex figure: Isosceles triangle, base 1, lateral sides
sqrt(2)
Schläfli symbols: t{2,3} or {3}x{ }
Wythoff symbol: 2 3 | 2
Symmetry group: Triangular dihedral [2,3], of order 12
Pentagonal prism
[10 vertices, 15 edges, 5 square and 2 pentagonal faces]
Vertex figure: Isosceles triangle, base tau, lateral
sides sqrt(2)
Schläfli symbols: t{2,5} or {5}x{ }
Wythoff symbol: 2 5 | 2
Symmetry group: Pentagonal dihedral [2,5], of order 20
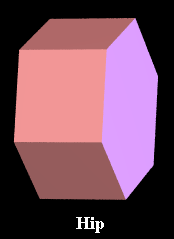Hexagonal prism
[12 vertices, 18 edges, 6 square and 2 hexagonal faces]
Vertex figure: Isosceles triangle, base sqrt(3),
lateral sides sqrt(2)
Schläfli symbols: t{2,6}, tr{2,3}, or {6}x{ }
Wythoff symbols: 2 6 | 2 or 2 2 3 |
Symmetry group: Hexagonal dihedral [2,6], of order 24
In nonprismatic convex uniform polychora, occurs only with
triangular dihedral symmetry
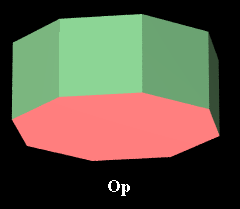Octagonal prism
[16 vertices, 24 edges, 8 square and 2 octagonal faces]
Vertex figure: Isosceles triangle, base
sqrt[2+sqrt(2)], lateral sides sqrt(2)
Schläfli symbols: t{2,8}, tr{2,4}, or {8}x{ }
Wythoff symbols: 2 8 | 2 or 2 2 4 |
Symmetry group: Octagonal dihedral [2,8], of order 32
In nonprismatic convex uniform polychora, occurs only with
square dihedral symmetry
Decagonal prism
[20 vertices, 30 edges, 10 square and 2 decagonal faces]
Vertex figure: Isosceles triangle, base
sqrt(2+tau), lateral sides sqrt(2)
Schläfli symbols: t{2,10}, tr{2,5}, or {10}x{ }
Wythoff symbols: 2 10 | 2 or 2 2 5 |
Symmetry group: Decagonal dihedral [2,10], of order 40
In nonprismatic convex uniform polychora, occurs only with
pentagonal dihedral symmetry
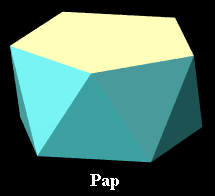Pentagonal antiprism
[10 vertices, 20 edges, 10 triangular and 2 pentagonal faces]
Vertex figure: Equilateral trapezoid, base sqrt(2),
the other three sides 1
Schläfli symbols: sr{2,5} or s{5}h{ }
Wythoff symbol: | 2 2 5
Symmetry group: Pentagonal antiprismatic [2+,10], of order 20
In nonprismatic convex uniform polychora, occurs as a
cell only in the grand antiprism
Also just for the record, a convex polytope is one with
this property: If a line segment’s end points both lie in
the polytope’s interior, then all the points on the line
segment between the end points also lie in the polytope’s
interior; and none of the faces overlap. A uniform polyhedron
is one whose faces are all regular polygons and any of whose
vertices (corners) may be transformed (or carried) into any of
its other vertices by its symmetries. A uniform polychoron
is one whose cells are all uniform polyhedra and any of whose
vertices may be transformed into any other of its vertices by its
symmetries. Not surprisingly, this definition easily extends to
n dimensions: a uniform polytope of n>4
dimensions is one whose facets (the elements of dimension
n–1) are uniform, and any of whose vertices may be
transformed into any of its other vertices by its symmetries.
(This property is called transitivity: the vertices of the
polytope are transitive under its symmetry group.) It should be
obvious that all the edges of any uniform polytope in n
dimensions have the same length, and that all the faces (elements
of dimension 2) are always regular polygons. Likewise, all the
vertices of an n-dimensional uniform polytope are
constrained by symmetry to lie on a single n-dimensional
sphere centered at the polytope’s center of symmetry. We may
further honor Archimedes by extending his name to the non-regular
uniform polytopes in n dimensions, just as the regular
n-dimensional polytopes may be referred to as
Platonic.
Pictures of all the non-prismatic uniform polyhedra, convex
and nonconvex, may be found at these websites: Roman
Maeder’s Uniform Polyhedra (also found, differently
organized, at All
Uniform Polyhedra), Steven
Dutch’s Uniform Polyhedra, Vladimir Bulatov’s
Polyhedra Collection, and
Virtual Reality Polyhedra (George
Hart). This discussion and the
usefulness of the accompanying tables will be greatly assisted if
the reader happens to have available an actual set of models of
the 18 Platonic and Archimedean polyhedra pictured above, all
matched to a unit edge length. A few matching prisms (triangular,
pentagonal, hexagonal, octagonal, and decagonal) and antiprisms
(particularly the pentagonal), also pictured above, wouldn’t
hurt, either. End of digression.
Contemplating the 18 convex uniform polyhedra that belong to
sets other than the infinite prismatic sets enchants us
three-dimensional viewers, so we might expect that contemplating
the analogous assemblage of 64 convex uniform polychora would
enchant a hypothetical four-dimensional viewer even more, because
the polychoric collection is markedly larger than the polyhedral
set, and some of the polychora are considerably more intricate.
The existence of exactly those 18 convex uniform polyhedra
is a fundamental property of three-dimensional Euclidean space,
and the existence of the 64 corresponding polychora is likewise a
fundamental property of four-dimensional Euclidean space. It is
only by thinking about and examining—by becoming familiar
with—the great variety of interesting polychora, not just
the regular ones (and particularly not just the tesseract,
or four-dimensional hypercube), that we can expand our ability to
visualize and handle such figures. (There is a website,
constructed by Melinda Green, where you can handle a
four-dimensional Rubik's Cube: 4D Rubik’s
Cube).
The convex Wythoffian polychora have been known since before
the 1920s through the work of Thorold Gosset, W. A. Wythoff,
Pieter Hendrick Schoute, E. L. Elte, and Alicia Boole Stott, and
systematized by H.S.M. Coxeter.
There is one anomalous, entirely non-Wythoffian
antiprismatic convex uniform polychoron, discovered by Conway and
Guy in 1965, that must also be added to complete the collection.
Using a computer search, they proved that the set described below
is indeed complete, and published the result in a short note
titled “Four-dimensional Archimedean Polytopes” in the
proceedings of a colloquium on convexity at Copenhagen.
Curiously, I’ve yet to see published an explicit table of
the convex uniform polychora and their properties, despite the
amount of time they’ve been known. So here for reference, at
this website, is such a table. The original version of these
tables was, as far as I know, the first to appear publicly
anywhere, in any medium.
For more on Coxeter, see the H.S.M. Coxeter home
page.
For plane and stereo views of projections of the six convex
regular polychora, go to Eric Swab’s
Website and click the appropriate buttons.
Click on the underlined text to access
various portions of the
Convex Uniform Polychora List:
Nomenclature: How the convex
uniform
polychora are named
List
Key: Explanations of the various List entries
Multidimensional Glossary:
Explanations of some geometrical terms and
concepts
Section
1: Convex uniform polychora based on the pentachoron
(5-cell): polychora #1–9
Section
2: Convex uniform polychora based on the tesseract
(hypercube) and hexadecachoron (16-cell): polychora
#10–21
Section
3: Convex uniform polychora based on the icositetrachoron
(24-cell): polychora #22–31
Section
4: Convex uniform polychora based on the hecatonicosachoron
(120-cell) and hexacosichoron (600-cell): polychora
#32–46
Section
5: The anomalous non-Wythoffian convex uniform polychoron:
polychoron #47
Section
6: Convex uniform prismatic polychora: polychora #48–64
and infinite sets
Section
7: Uniform polychora derived from glomeric tetrahedron
B4: all duplicates of prior
polychora
Let me know what you think about my
page. Send mail by clicking here.
This page has been visited
times. The counter was scrambled for unknown reasons
February 5, 1998 and had to be reset. Then it was scrambled again
on May 30, 2003 and had to be reset, and yet again
on March 1, 2006, once more on November 28, 2006,
again on December 19, 2006, and again on January 31, 2007.
This is driving me positively crazy!
Anyway, add 82250 to the
above number for a more accurate count.
Text ©1997 George Olshevsky, but
the math belongs to everyone.
Just added November 22, 2004: A website where you can view and even purchase beautiful
prints of interesting polychora nets. Go to Nuts About Nets!
Name and Location:
