which maximizes 
Problems related to university entrance examination apparently are critical for every university. In fact, any change in entrance examination often exerts serious effects on university education. Hence, many endeavors to improve entrance examination have been cautiously administered from various points of view.
In our country, the selection of applicants for admission to university is based on a composite score of two examinations. One is a common first-stage examination called ``The National Center Test for University Admissions'' (First-stage Examination; FE), and the other is a second-stage examination (Second Examination; SE) administrated by each university. The composite score is normally a weighted sum of marked scores for these two examinations, and the weights for the composite score are determined by each university.
In addition to receiving the above two examinations, the applicants are requested to show their high-school report (HR). However, the high-school marks usually are not considered explicitly for the selection of applicants, perhaps because there exists no decisive method to adopt HR effectively.
We here propose a new method to determine a composite score which depends not only on FE and SE but also on HR. The method is based on the Convex Cone Method (Hashimoto, Miyano, & Taguri, 1997), and gives an optimal composite score in a sense that the correlation of the composite score and university records is maximized under given appropriate constraints.
The Convex Cone Method developed by Hashimoto et al. (1997) gives an exact solution of the following optimization problem.
(Problem 1). Find
which maximizes
subject to the constraint
where 
is a symmetric positive definite matrix,
are nonzero vectors and
is a Euclidean norm.
In case of entrance examination, 
corresponds to unknown weight
vector of which elements are the weights for a composite score, and
is the vector corresponding to average university records. And the
constraint means that the optimal weight should not be much different from
corresponding current weight vector 
.
Let 
be a given vector of which elements denote the
average university records of selected applicants where n is the number of
the selected, and 
and 
be matrices whose
elements denote the scores for HR, FE and SE respectively, where 
and 
are the numbers of
subjects included in HR, FE and SE. For each of these matrices, we
introduce unknown weight vectors 
for 
i=0,1,2, to define a composite score 
by
where 
and 
For
the evaluation of weight vectors, we consider a correlation
coefficient between 
and
;
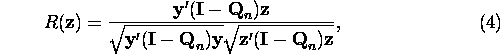
where 
and 
The
correlation coefficient may be more appropriate for the evaluation of weight
vectors than a squared distance between
and , since
subjects administered in entrance examination have not always equal full
marks and the squared distance is affected by the different choice of full
marks.
Considering the normalization of the weight vectors and the condition that weight vector much different from a current weight vector may be unfavorable, we assume the following two constraints;
where 
is a current weight vector, and 
is a symmetric positive definite matrix. In
addition to these two constraints, without loss of generality we can
assume
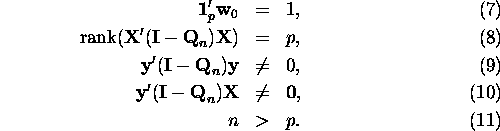
Eventually our problem can be formulated as a optimization problem under nonlinear constraints:
(Problem
0). Find 
which maximizes 
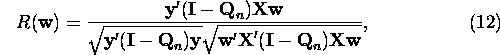
subject to the constraints,
Numerical solution of our problem, problem 0, can be obtained
by using the Convex Cone Method (Hashimoto et al. 1997). Of course the
Convex Cone Method can not be applied to our current problem directly,
since our problem includes the constraint 
in addition to a quadratic
constraint. After tedious considerations on several cases defined by
the given constraints, we however can assert that our problem can be
numerically solved by the Convex Cone Method.
We here give a
numerical example to illustrate our method. Analyzed data were
artificial but partly borrowed from real entrance examination
data. The following shows a summary of the analyzed data:
n=100, 
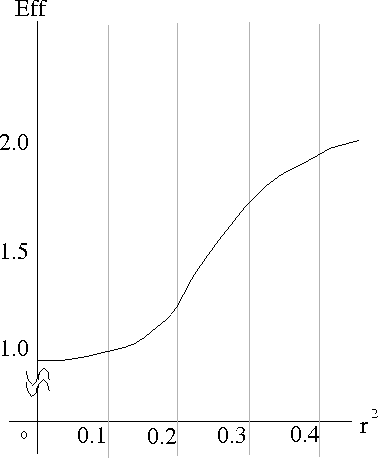
Figure 1 shows relative changes of 
with different 
where 
is a solution of
problem 0;
that is, in
order to compare the optimal weight
with the current weight
we
calculated the efficiency ratio defined by
Note
that 
and
.
In this paper, we proposed a method to determine an optimal composite score which can be used for the selection of applicants for admission to university. Our method has an advantage that it can consider a realistic condition that any drastic change of weight vector may exert unfavorable effects to university education.
While we may say
that our method is effective on the whole, there still remains some
problems to be solved. The most important one is a problem related to
the estimation of 
and
. These values
should be estimated from the data of selected applicants. We however have no
decisive method to estimate these values.
